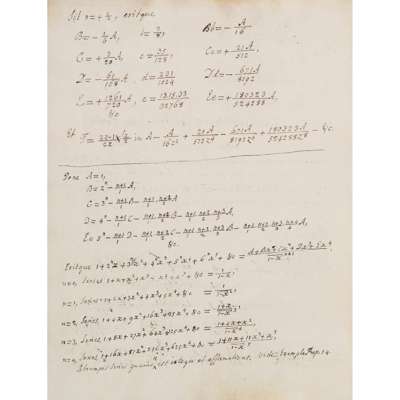Lot 53

Stirling, James (1692-1770)
Methodus Differentialis sive Tractatus de Summatione et Interpolatione Serierum Infinitarum



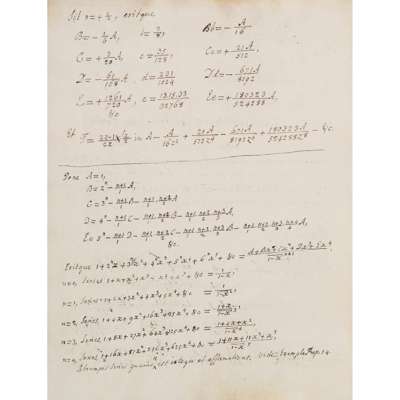








The Library of James Stirling, Mathematician
Auction: 23 October 2025 from 13:00 BST
Description
London: typis Gul. Bowyer, impensis G. Strahan, 1730. First edition, 4to in half-sheets (27.5 x 21.3cm), contemporary mottled calf, [6] 13 [1] 15-153 [1] pp., woodcut head- and tailpieces and initials, diagrams in text, binding rubbed, wear to spine, partial splitting to joints, a sliver of thumbing to lower margins, a few other old marks and blemishes internally [ESTC T110104; Wallis 307.882]
Footnote
First edition, James Stirling's personal working copy of his masterpiece and ‘principal contribution to mathematics’ (ODNB), with his ownership inscription to the title-page, four pages of autograph annotations to the rear blanks, and autograph marginalia to some 50 pages, ranging from corrections of typographical errors to substantial additions to the text. Evidently a large-paper copy: Bowyer's ledgers records 26 copies printed on royal, and 425 standard copies printed on crown.
The Methodus differentialis is a greatly expanded version of Stirling's ‘Methodus differentialis Newtoniana illustrata’, a paper which he communicated to the Royal Society in 1719 in response to Newton's own ‘Methodus differentialis', which had been written in 1676 but was not published until 1711 with its inclusion by William Jones in the Analysis per quantitatum series, fluxiones, ac differentias. During the 1720s Stirling was busy with his work as a tutor at Watts's Academy in Little Tower Street, Covent Garden, delaying his completion of the text, a situation on which he remarked in a letter written to Gabriel Cramer in 1730 accompanying presentation copies for Cramer and Nicolaus Bernoulli (see lot 21 and Tweddle, 2003, p. 3):
‘The first part has been written 8 or 9 years ago, so that if I were to write it again I should scarce change anything in it; But indeed that is more than I can say for the second part, because there was not above one half of it finished, when the beginning of it was sent to the printer. And altho’ I am not conscious of any errors in it but typographical ones, yet I am sensible that it might have been better done.'
This copy was consulted by mathematician and historian of mathematics Ian Tweddle for both his annotated English edition of the text, which incorporates Stirling’s autograph corrections and additions, and a broader study of Stirling’s work based on his manuscripts and notebooks. Stirling’s notable marginalia include a detailed footnote to pp. 120-1 elaborating the remark in Proposition 23 that ‘in practice it is not necessary to have recourse to series, for it suffices to take the proportional mean between the semicircumference of the circle and n + ½’ (Tweddle, 1988, p. 50). His annotations to the blanks include demonstrations of three variants of Proposition 28 using Abraham de Moivre’s second series, and of a further case of a problem whereby, ‘given a sequence of numbers z in arithmetic progression and a functional relation between the values T and T’ of a function at successive values of z’, it is proposed to find a series to represent the function at intermediate values of z (ibid., p. 94).
The introductory section of the Methodus contains 'Stirling's discussion of what are now called "Stirling numbers" (important in modern combinatorial theory) and in example 2 of proposition 28 there is his version of ‘Stirling's formula’ for approximating to the logarithm of a large factorial (an early example of an asymptotic series)' (ODNB). ‘The Methodus differentialis … is surely one of the early classics of numerical analysis. It contains not only the results and ideas for which Stirling is chiefly remembered today (the Stirling numbers, Stirling’s interpolation formula, Stirling's formula for ln n!), but also a wealth of material on transformations of series and limiting processes. Inverse factorial series, especially hypergeometric series, are much in evidence and asymptotic series … also appear. Interpolation and quadrature are discussed and there is an impression collection of calculations throughout to illustrate the efficacy of the methods presented. Stirling's book was well received by his contemporaries … [and] the book's influence has extended over more than two and a half centuries' (Tweddle, 2003, p. 1)
Literature:
Ian Tweddle (ed.), James Stirling's Methodus Differentialis: An Annotated Translation of Stirling's Text, London, 2003.
ibid., James Stirling: ‘This about Series and Such Things’, A Discussion of the Later Works of Scottish Mathematician James Stirling (1692-1770), based mainly on Material from his Notebooks, Edinburgh, 1988, pp. 13-14, 50, 56-8, 95-8.
Niccolo Guicciardini, The Development of Newtonian Calculus in Britain 1700-1800, Cambridge, 1989, p. 33 et seq.