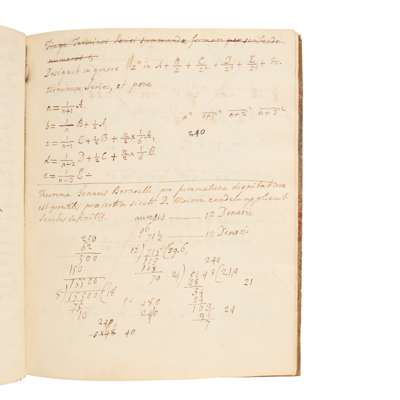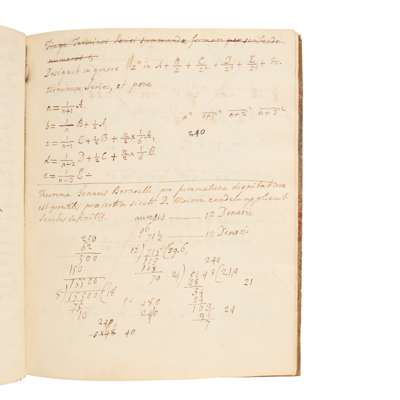Lot 51

Stirling, James (1692-1770)
Mathematical notebooks
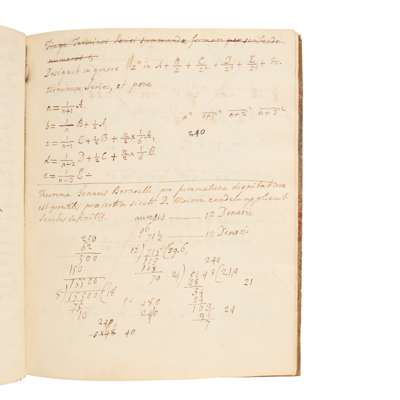




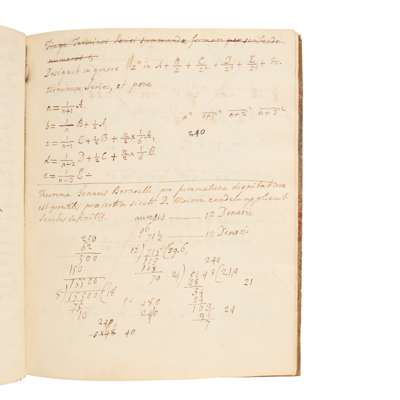






The Library of James Stirling, Mathematician
Auction: 23 October 2025 from 13:00 BST
Description
3 holograph notebooks, comprising:
1) Folio (30 x 20cm), contemporary comb-marbled wrappers, [35] ff., f. [1] loose, in ink and pencil, with diagrams throughout, partial ownership inscription ‘James Stirl’ on f. [2], inside rear wrapper with two lists of names of mathematicians and other figures under headings ‘Books Given to’ and ‘Not yet given’, presumably referring to copies of the Methodus differentialis (1730), recipients including Moivre, Pemberton, Mclaurin (sic), N Bernouilli, Cramer, Bradley, and Halley, Jones, Pemberton, Klingenstierna, Taylor, and others, other contents including:
ff. [1-12], a series of propositions on circle geometry;
ff. [13-14] notes on Isaac Newton’s Tractatus de Quadratura Curvarum;
f. [21] ‘A table of Areas of Binominal Curves’;
ff. [31-32], notes on ancient shipbuilding and astronomy with reference to the Bible, Apollonius, the Egyptians, Diodorus Siculus
2) Folio (31.8 x 20cm), contemporary comb-marbled wrappers, [37] ff., front wrapper near detached, contents include:
f. [1] notes and calculations on pendulums and gravity;
f. [3] Lemma on ellipses (‘Suppose now the breadth of the elliptic ring AFBEMD to be infinitly diminished; and any two ordinates whatsoever to be drawn infinitly near’);
ff. [4] et seq., headed ‘To find the direction and quantity of the force of gravity on the surface of an oblate spheroid’, with diagrams and profuse equations;
with 1 f. at rear headed ‘Section I. Of the magnitude of the Earth according to the Antients’;
3) 4to (22.4 x 17.8cm), contemporary calf-backed comb-marbled boards with vellum tips, annotated on front board ‘This about Series and Such things’ apparently in James Stirling's hand, [83] ff., approx. 15 diagrams and graphs, contents include:
ff. [5-7], on the relation between solar years and lunar periods including reference to Scaliger, in Latin and English;
ff. [8-39], extensive notes on infinite series, with demonstrations, in Latin, begins ‘Theorema Joannis Bernoulli pro summatione dignitatam est perutilis sicuti D. Moivre eandem applicuit seriebus infinitis’ (‘The theorem of Johann Bernoulli for the summation of series is very useful as D. Moivre applied it to infinite series’); f. [11], ‘Regula pro formatio numerorum D[omi]ni Bernoulli pro summatione postestatum’ (‘Mr Bernoulli’s rule for the formation of numbers for the summation of powers’); f. 39 concludes ‘De hoc theoremata haec sunt notanda, quod ubi series quae summanda proponitur sit magnitudine finitatum summa hic assignata pure sumpta est eiusdem valor, at ubi series est magnitudine infinita, quod accidit quando est n major unitate, vel etiam quando est n unitas ut in casu secundo, quando n est unitas vel minor unitate vel numerus negativus’;
ff. [39-40], lists of natural logarithms;
ff. [40-52], notes on mechanics and gravity, in English and Latin, focusing on the oscillation of a pendulum in a cycloid and its application to measuring figure of the earth, noting measurements taken at Pello, Jamaica, Paris, London (e.g. f. [42]: ‘The force of gravitation on the surface of a planet is to the centrifugal force, in a ratio compounded of the duplicate ratio of the periodic time of a satellite to the diurnal revolution of the plan inversely, and directly of the triplicate ratio of the distance of the satellite to the semidiameter of the planet’);
ff. [52-4], ancient measures;
f. [54] et seq., notes on fluxions and series, ‘Determination coefficientium’ and ‘coefficientes adductae’ (coefficient of determination and adduced coefficients, ff. [60]-[61];
f. [69], notes on ancient measures from Pococke;
with [14] ff. at front and rear comprising accounts for Leadhills mines including payment of workers, 1741-3, and a laid-in autograph memorandum on smelting at Leadhills, dated 15 May 1735, beginning ‘The famous tryal betwixt the furnace and mills is now over …' (foolscap bifolium, 4 pp.).
Footnote
A microcosm of the variety and extent of James Stirling's intellectual labours, these notebooks contain workings on all his principal areas of interest, including series, geometry, gravity and the figure of the earth, and weights and measures. The inclusion in one notebook of methodical accounts for the mines at Leadhills foreshadows the path of his later career, whereas the attention to oscillation and pendulums recalls the subject of his first known letter to Newton, written from Venice in 1719 and published in Brewster's Memoirs ('I beg leave to let you know, that Mr. Nicholas Bernoulli proposed to me to enquire into the curve which defines the resistances of a pendulum, when the resistance is proportional to the velocity').
All three notebooks were consulted by mathematician and historian of mathematics Ian Tweddle for his 1988 work James Stirling: On Series and Such Things, where they are referred to respectively as G2, G3 and G6. Tweddle's study contains brief summaries of each notebook as well as selective analyses of their mathematical content. Notebook 1/G2 probably dates from c.1730 in light of the list of mathematicians' names presumed to be list of recipients of the Methodus differentialis, which appeared in that year; 2/G3 is ‘probably from the mid 1730s with later additions’ (Tweddle, p. 3), 3/G6 contains accounts for Leadhills mines dated 1741 and 1743, though the other content, much of which relates to the Methodus, possibly ‘predates the accounts’ (ibid., p. 4).
Literature:
Ian Tweddle, James Stirling: ‘This about Series and Such Things’, A Discussion of the Later Works of Scottish Mathematician James Stirling (1692-1770), based mainly on Material from his Notebooks, Edinburgh, 1988.